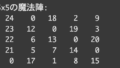はじめに
こんにちは、Yuinaです🌰
今日は、令和3年度度秋期の応用情報第3問の疑似言語をPythonに書き換えてみます。
すべての辺を一度ずつ通る、つまり一筆書きの経路を一つ見つける問題ですね。
では、やっていきましょう。よろしくお願いいたします!
コード
from collections import deque
# --- データの定義 ---
N=6 # 点の数
M=8 # 辺の数
# 頂点番号が1から始まることを想定して、データを調整
start = [0, 1, 2, 3, 4, 2, 5, 4, 6] # 各辺の始まりの点
end = [0, 2, 3, 4, 1, 5, 4, 6, 2] # 各辺の終わりの点
# [0] [1(a)] [2(b)] [3(c)] [4(d)] [5(e)] [6(f)] (点番号)
edgefirst = [0, 1, 2, 3, 4, 6, 8] # 各点から最初に出るべき辺の番号
edgenext = [0, 0, 5, 0, 7, 0, 0, 0, 0] # ある辺の次に続くべき辺の番号
# --- 記録用の配列 ---
# 頂点番号 1〜N を使うため、サイズは N+1 にする
current = [0] * (N + 1)
# 辺の番号 1〜M を使うため、サイズは M+1 にする
searched = [0] * (M + 1)
path = [0] * (M + 1)
# --- 処理 ---
def directedE():
# edgefirstのインデックス0をダミーとして無視し、1からNまでをコピー
for i in range(1, N + 1):
current[i] = edgefirst[i]
top = 1
last = M
x = 1
# すべての辺がpathに記録されるまで、このループが繰り返される
while(last >= 1):
# まだ進める道がある場合
if(current[x] <= M and current[x] != 0):
# 今から進む辺の番号をtempに保存
temp = current[x]
# searchedのメモに、この辺を通ったことを記録
if top <= M:
searched[top] = temp
top = top + 1
# currentのメモを更新し、次にこの点に戻ってきたときのために、次の道を設定
current[x] = edgenext
# 今通った道の終点に移動 (start/end もインデックス1から辺のデータがあると仮定)
x = end
else:
print("Error: Searched stack overflow")
return
# 行き止まりになった場合
else:
if top > 1:
# searchedのメモを一つ前に戻す
top = top - 1
# 一つ前に戻った辺の番号をtempに保存
temp = searched[top]
path[last] = temp
# 今確定した辺の始まりの点に戻る
x = start
# pathのメモの次の場所に書き込めるようにする
last -= 1
else:
print("Error: Searched stack underflow (全ての経路を探索済みか、初期点で詰まった)")
return
print("一筆書きの経路:",path[1:])
directedE()
解説
directedEメソッド
このメソッドは、一筆書きの経路を見つけるためのメインの処理です。
def directedE():
for i in range(N):
current[i] = edgefirst[i]
top = 0 #
last = M - 1
x = 0
まず、各点から最初に出るべき辺(edgefirst[i])をcurrent[i]にコピーし、最初の道を選べるようにします。
topはsearchedのメモに書き込む場所を管理します。
lastはpathのメモに書き込む場所を管理します。
xは現在いる点を示します。(最初は点1からスタート)
while(last >= 0):
すべての辺がpathに記録されるまで、このループが繰り返されます。
(0番目の要素をダミーとして追加することで、元のコードの1から始まる添字のロジックを保ったまま実行できます。)
まだ進める道がある場合、以下の処理を行います。
if(current[x] < M and current[x] != 0):
temp = current[x]
if top < M:
searched[top] = temp
top = top + 1
current[x] = edgenext
x = end
まず、今から進む辺の番号をtempに保存します。
if top < Mについてですが、topは配列searched をスタックとして扱う際の「次に書き込むべき場所(スタックの先端)」を指すインデックスです。「top < M」は配列(サイズM)に空きがある状態を示しています。
次に配列searchedのメモに、この辺を通ったことを記録します。
current[x] = edgenextでは、次にこの点に戻ってきたときのために、次の道を設定します。
x = endでは、配列endにtempを指定することで今通った道の終点に移動します。
続いて、行き止まりになった場合の処理を確認しましょう。
このブロックは、主に「①一時記録用のスタックから辺を取り出す」→「②その辺を最終経路に確定させる」→「③その辺の始点に戻る」という3つのステップで構成されます。
# if(current[x] <= M and current[x] != 0)がFalseの場合
else:
if top > 1:
top = top - 1
temp = searched[top]
path[last] = temp
x = start
last -= 1
else:
print("Error: Searched stack underflow (全ての経路を探索済みか、初期点で詰まった)")
return
if top > 1は、配列searchedにまだsearched スタックにまだ戻れる辺が残っているかを確認します。(ここでは top = 1 が空の状態を意味すると仮定しています)。
①一時記録用のスタック(searched)から辺を取り出す
top = top – 1で、一つ前に戻ります。
temp = searched[top]で戻った辺の番号をtempに保存します。
②その辺を最終経路(path)に確定させる
path[last] = tempで、最終的な結果を記録する 配列pathにtempを書き込みます。
このアルゴリズムは、経路を逆順で確定させます。これは、DFSで「行き止まりになった最後の辺から」確定していくためです。
③その辺の始点に戻る
x = start で、確定した辺の始まりの点に戻ります。
例えば、temp は点Aから点Bへ進みましたが、点Bで行き詰まったとしましょう。探索を続けるために点Aに戻る必要があります。点Aに戻ることで、点Aから出る別の未踏の辺がないか、探索を再開できます。
最後に、last -= 1でpathスタックのポインターを1ずつ減らします。これは、次の場所にメモを書き込めるように、pathのスタックを空いている位置に移動しています。
出力結果
結果はこのようになりました。

ありがとうございました✨