はじめに
こんばんは🌛Yuinaです。
今日は応用情報の疑似言語をPythonに書き直してみました。
間違ってるかもしれませんが、最後まで書いてみたのでよかったらご覧ください。
作成したコード
from collections import deque
def treeSearch(target: int, numbers: list) -> int:
class Status:
def __init__(self, total, selected_numbers, next_index):
self.total = total
self.selected_numbers = selected_numbers
self.next_index = next_index
queue = deque()
currentStatus = Status(total=0, selected_numbers=[], next_index=0)
queue.append(currentStatus)
ansStatus = None
while queue:
currentStatus = queue.popleft()
if ansStatus is None:
ansStatus = currentStatus
elif abs(target - ansStatus.total) > abs(target - currentStatus.total):
ansStatus = currentStatus
if currentStatus.next_index < len(numbers):
nextStatus1 = Status(
total = currentStatus.total + numbers[currentStatus.next_index],
selected_numbers = currentStatus.selected_numbers + [numbers[currentStatus.next_index]],
next_index = currentStatus.next_index + 1
)
queue.append(nextStatus1)
nextStatus2 = Status(
total = currentStatus.total,
selected_numbers = currentStatus.selected_numbers,
next_index = currentStatus.next_index + 1
)
queue.append(nextStatus2)
return ansStatus.total
if __name__ == "__main__":
numbers = [10, 34, 55, 77]
target = 100
result = treeSearch(target, numbers)
print(f"目標値 {target} に最も近い合計は {result} です。")
解説
def treeSearchメソッド
こちらのメソッドでは、与えられた数のリストから合計が目標値に最も近くなる組み合わせの合計を見つけます。
幅優先探索(BFS)アルゴリズムに基づいているので、メソッド名をtreeSearchと命名しました。
def treeSearch(target: int, numbers: list) -> int:
class Status:
# 初期化
def __init__(self, total, selected_numbers, next_index):
self.total = total
self.selected_numbers = selected_numbers
self.next_index = next_index
関数の中にクラスがありますが、このように定義されたクラスをローカルクラスと呼びます。
ローカルクラスを使うことで、このクラスが他の場所で使われる可能性がなくなったり、コードの意図が明確になったりして、汎用的なデータ構造と混同されることを防げます。
また、treeSearchの外側からはアクセスできません。これにより、開発者が誤ってこのクラスを他の用途に使用したり、別のクラス名と衝突(名前の重複)したりするのを防ぐことができます。
queue = deque()
currentStatus = Status(total=0, selected_numbers=[], next_index=0)
queue.append(currentStatus)
ansStatus = None
ここでは、BFSの核となるデータ構造であるキューを用意しています。
次に探索の「スタート地点」となる最初の状態オブジェクトを定義します。
そこに初期状態をキューに追加します。
そして、最も目標値に近いと判断された状態を記録するansStatusを宣言します。
while queue:
currentStatus = queue.popleft()
if ansStatus is None:
ansStatus = currentStatus
elif abs(target - ansStatus.total) > abs(target - currentStatus.total):
ansStatus = currentStatus
キューが空になるまで、キューから一番古い状態(先頭にある状態)を取り出して、currentStatusに入れます。
次に、答えの候補を更新する処理を行います。
最も目標値に近い値がまだ決まっていない場合、最初に調べたcurrentStatusを暫定的な答えとします。
現在の答えの候補(ansStatus)よりも今見ている状態(currentStatus)の方が目標値に近い場合、答えの候補をcurrentStatusに更新します。
if currentStatus.next_index < len(numbers):
このセクションでは、探索ツリーを広げ、次に調べるべき新しい状態を生成します。
まだ調べていない数字が残っているかを確認し、「選ぶ」という行動の結果として生まれる新しい状態 (nextStatus1) を作成しています。
(※queue.append(nextStatus1)の前までは、「もしこの数字を選んだら、次の状態はどうなるか?」という未来の状態を計算しています。)
nextStatus1 = Status(
total = currentStatus.total + numbers[currentStatus.next_index],
selected_numbers = currentStatus.selected_numbers + [numbers[currentStatus.next_index]],
next_index = currentStatus.next_index + 1
)
queue.append(nextStatus1)
「選ばない」という行動の結果として生まれる新しい状態 (nextStatus2) を作成しています。
(※queue.append(nextStatus2)の前までは、「もしこの数字を選ばなかったら、次の状態はどうなるか?」という未来の状態を計算しています。)
nextStatus2 = Status(
total = currentStatus.total,
selected_numbers = currentStatus.selected_numbers,
next_index = currentStatus.next_index + 1
)
queue.append(nextStatus2)
図で表したものが下記の通りです。
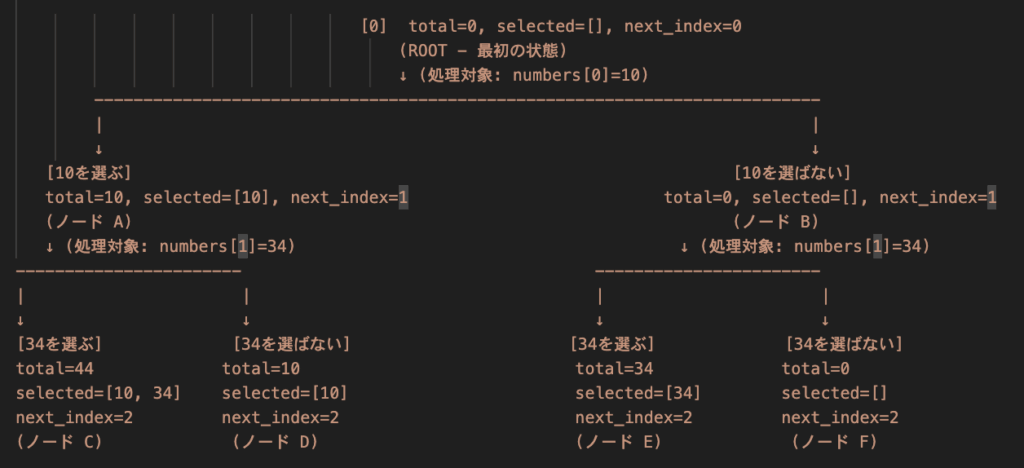
[数字を選ぶ/選ばない]: そのノードに至るために、next_indexで示されるnumbersリストの数字を「選んだ」か「選ばなかった」かを示します。total: その時点での合計値。selected: その時点までに選ばれた数字のリスト。next_index: 次に処理すべきnumbersリストのインデックス。
return ansStatus.total
全ての探索が終了したら、最も目標値に近かった合計値を返します。
実行結果

10, 34, 55, 77のどの数字かを組み合わせた合計でが100に最も近いのは99となりました。
ありがとうございました✨

