はじめに
こんばんは。Yuinaです!
今日は符号付き2進数の掛け算を、ビット列の見た目でわかりやすく確認できる、計算アプリ風のPythonコードを作成しました。
よろしくお願いいたします!
符号付き乗算の計算手順
①2の補数表現への変換します!(準備)
計算を始める前に負の数があれば2の補数表現に直します!
1.かけられる数とかける数を、それぞれ決めたら2進数で表現します。
2.負の数の場合、絶対値のビットを反転し、1を加算します。
3.正の数の場合、そのままです。
②通常の符号なし乗算を実行します!
「①2の補数表現への変換(準備)」で用意した2つのビット列を、符号がない普通の正の数のように扱います。
1.筆算の領域で通常の掛け算をします。
③結果のビット幅(例:8ビット)を2Nに拡張します(重要!)
1.乗算の結果を格納する箱を、元のビット幅の2倍(例:8 x 8 = 16ビット)にします。
④符号拡張を適用し、最終結果を得ます!
結果のビット列が正しい2の補数になっているかを確認します。
1.もしステップ2の結果が負の数なら、左の余ったビットを1で埋めます。(符号拡張)
2.もしステップ2の結果が正の数なら、左の余ったビットを0で埋めます。
コード
def decimal_twos(value, bits):
max_signed_value = (1 << (bits - 1)) - 1
min_signed_value = -(1 << (bits - 1))
if value > max_signed_value or value < min_signed_value:
print(f"値 {value} は {bits}ビット(符号付き)で表現できないよ!")
if value < 0:
two_comp_val = (1 << bits) + value
return format(two_comp_val, f'0{bits}b')
else:
return format(value, f'0{bits}b')
def multiplier_app(num1, num2, input_bits=8):
output_bits = input_bits * 2
print(f"設定: 入力 {input_bits}ビット ➡ 結果 {output_bits}ビット")
bin1 = decimal_twos(num1, input_bits)
bin2 = decimal_twos(num2, input_bits)
print(f"STEP 1: 2の補数に変換")
print(f" {num1}: {bin1} (符号ビット: {bin1[0]})")
print(f" {num2}: {bin2} (符号ビット: {bin2[0]})")
result_decimal = num1 * num2
result_bin = decimal_twos(result_decimal, output_bits)
print(f"\nSTEP 2 & 3: 掛け算と符号拡張")
print(f" 10進数での答え: {num1} × {num2} = {result_decimal}")
print(f" {output_bits}ビットの最終ビット列:")
print(f" {result_bin}")
multiplier_app(-5, 3, input_bits=8)
解説
🌻decimal_twosメソッド
こちらのメソッドは10進数を指定ビット幅の2の補数バイナリ文字列に変換しています。
まず、表現範囲を決めます。
max_signed_value = (1 << (bits - 1)) - 1
min_signed_value = -(1 << (bits - 1))
max_signed_valueはNビットで表現できる最大値 (2^(N-1) – 1)で、min_signed_valueは Nビットで表現できる最小値 (-2^(N-1))です。
| 定義式 | 計算 | 10進数での結果 | 2進数での表現 (8ビット) |
最大値 (max_signed_value) | 2^(8−1)−1=2^7−1 | +127 | 01111111 |
最小値 (min_signed_value) | −2^(8−1)=−2^7 | −128 | 10000000 |
続いて、負の数(2の補数)を計算します。
if value < 0:
two_comp_val = (1 << bits) + value
return format(two_comp_val, f'0{bits}b')
two_comp_valはビット操作と足し算を組み合わせて、負の数を2の補数に変換するためのものです。
1<< bitsでは、桁を2bits(2N)を計算します。これは、たとえば N=8 ビットなら 256 で、これは 8 ビットで表現できる最大の数 11111111 の次の桁を意味しています。
+ value では、負の数(例:−5)を足しているので、実質的には 2N−∣value∣ という引き算になります。(例: 256+(−5)=256−5)
なぜこれで2の補数になるかというと・・・
手作業でやる 「ビット反転してから +1 する」 という計算は、(2N−1)−∣value∣+1 という式と同じだからです。

なので、コンピュータは面倒なビット反転をせずに、一回の足し算(引き算)でマイナスの数値を2の補数に変換できます。
メソッドの最後に、formatで指定ビット幅のバイナリ文字列にしています。
return format(two_comp_val, f'0{bits}b')
🌻multiplier_appメソッド
output_bits = input_bits * 2
print(f"設定: 入力 {input_bits}ビット ➡ 結果 {output_bits}ビット")
bin1 = decimal_twos(num1, input_bits)
bin2 = decimal_twos(num2, input_bits)
このメソッドでは、まず桁あふれ防止と符号拡張のためのスペース確保のため、2Nビット化します!
拡張符号についてもう少し具体的に説明します。
例えば、8ビットの −5 は 11111011 ですよね。もし、これを 0 で拡張すると…

左端が 0 になった瞬間、この数は正の数になってしまいます。
なので、負の数のビット列を広げるときは、左端の 1 をそのままコピーして埋める必要があります。

2Nビット化の後は、num1,num2を2の補数に変換します。
result_decimal = num1 * num2
ここでは、普通に掛け算します。
result_bin = decimal_twos(result_decimal, output_bits)
上で乗算したresult_decimaと2Nビット化されたoutput_bitsを10進数を指定ビット幅の2の補数バイナリ文字列に変換に変換します。
この時符号拡張と結果が2Nビットで表現可能かどうかチェックされます。
実行結果
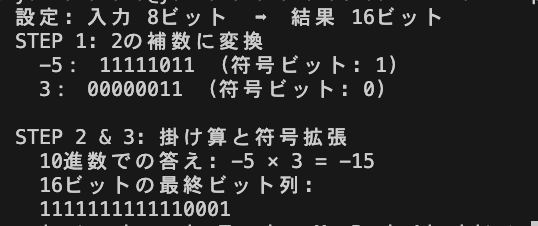
結果は上のようになりました。
ありがとうございました✨

